Notes on Vector Calculus

This post contains some of the important notes which come in handy while working with vector-calculus.

Vector Space

A vector space is a collection of objects called vectors, which may be added together and multiplied/scaled by scalars. Scalars are often taken to be real numbers.

\[\mathbf{x} = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix}\]

\(\mathbf{x}\) is a vector of \(n\) dimensions.

Function

A function is relationship between two sets. It associates an element from frist set to exactly one element of second set.

\[f: \mathit{X} \rightarrow \mathit{Y} \label{eq1}\] \[\mathbf{x} \mapsto f(\mathbf{x}) \label{eq2}\]

In equation \eqref{eq1}, the set represented by \(\mathit{X}\) is called domain of function \(f\) and \(\mathit{Y}\) is called codomain of function \(f\). This notation can be read as ‘the function \(f\) mapping elements of set \(\mathit{X}\) to elements of set \(\mathit{Y}\)’. Similarly, \eqref{eq2} can be read as ‘\(f\) maps \(\mathbf{x}\) to \(f(\mathbf{x})\)’.

Scalar-valued function or Scalar field

The function which maps a vector to a scalar value.

\[f:\Re^n \rightarrow \Re \label{eq3}\] \[y = f(\mathbf{x}) \label{scalar-func}\]

Equation \eqref{eq3} maps an \(n\)-dimensional vector to a scalar value. It is a scalar-valued function. \(y\) is a scalar and \(\mathbf{x}\) is a vector of \(n\)-dimensions in \eqref{scalar-func}.

Vector-valued function

A vector-valued function maps one vector space to another vector space.

\[\mathbf{f}: \Re^n \rightarrow \Re^m \label{eq4}\] \[\mathbf{y} = \mathbf{f}(\mathbf{x}) \label{eq5}\]

Equation \eqref{eq4} maps an \(n\)-dimensional vector to a vector of \(m\)-dimensions. It is a vector-valued function. The output value \(\mathbf{y}\) in \eqref{eq5} is of \(m\)-dimensions and the corresponding input value \(\mathbf{x}\) is of \(n\)-dimensions.

Gradient

The gradient of a scalar-valued differentiable function is also referred to as vector field or vector-valued function.

\[\bigtriangledown f: \Re^n \rightarrow \Re^n \label{eq-grad1}\]

Gradient of vector-valued function at a point \(\mathbf{x}\) in domain \(\mathit{X} \in \Re^n\) is:

\[\bigtriangledown f(\mathbf{x}) = \begin{bmatrix} \frac{\partial f}{\partial x_{1}} \\ \frac{\partial f}{\partial x_{2}} \\ \vdots \\ \frac{\partial f}{\partial x_{n}} \end{bmatrix}\label{eq-grad2}\]

At each point of a scalar-valued function, a gradient is a tangent vector representing an infinitesimal change in vector input. Notice that here a column vector is used to represent the gradient of the function at point \(x\).

Derivative

Derivative at each point of the scalar-valued function is a co-tangent vector, a linear form that expresses how much the scalar output of a function changes for a given infinitesimal change in the input vector. Notice, we represent the derivative of a scalar-valued function as a row vector. This is unlike the gradient vector (that used column vector).

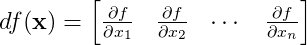
\(\label{eq-derivative1}\)

Note: derivative is just a transpose of gradient.

\[df(\mathbf{x}) = \bigtriangledown f(\mathbf{x})^{T} \label{eq-derivative2}\]

Linear approximation of a scalar-valued function

Linear approximation of a function \(f(\mathbf{x})\) at a point \(\mathbf{x_{0}} \in \Re^{n}\):

\[f(\mathbf{x}) \approx f(\mathbf{x_0}) + (\bigtriangledown f)_{\mathbf{x_0}} (\mathbf{x} - \mathbf{x_0})\]

Jacobian (a.k.a. derivative of Vector-valued Function)

Derivative of \(\mathbf{f}\) in equation \eqref{eq5} linearly maps tangent space \(T_{\mathbf(x)}\) to tanget space \(T_{\mathbf(y)}\).

First order-partial derivative of vector-valued function forms the Jacobian matrix. We will denote the Jacobian by the notation \(\mathbf{J}\)

Note: Jacobian has the dimensions of \(m \times n\).

A Jacobian is the vertical stack of derivative vectors corresponding to each output element of vector \(\mathbf{y}\) (i.e., row of the Jacobian matrix). This definition makes sense, and we can relate it to the derivative of a scalar-valued function defined above. The derivative of a scalar-valued function, \(m=1\), is a row vector.

Hessian matrix

Hessian matrix for scalar-valued function or scalar field given by \eqref{scalar-func} is a square matrix of second order partial derivatives of this scalar-valued function.