Rotation using Euler Angles

I have always found rotation using Euler angles confusing. This post is just a simple note to maintain my sanity while performing rigid body transformations using Euler angles and rotational matrices.

Rotation

Rotational matrices are special orthogonal matrices. I am not going to discuss any property of these matrices over here. But this post is a quick reference for rotation using z-y-x Euler angles. For further details, you can refer to this.

Euler Angle Transformation

The most important thing you must remember before reading further about transformations using Euler angles is:
The order of matrix multiplication of rotational matrices is of extreme importance.

1. Euler angles are used to specify the orientation of one reference frame relative to another reference frame.
2. Euler angles are specified by the three angles, viz., $\psi$, $\theta$, $\phi$.
3. Euler angles represent three consecutive rotations in the order of $\psi$, $\theta$, $\phi$ so that one coordinate axes system is made to coincide with another system.
4. Again, the order of rotation, i.e., $\psi$, $\theta$, $\phi$, is very very important.
5. Angle $\psi$ - Angle to be rotated about the current frame's Z-axis.
6. Angle $\theta$ - Angle to be rotated about the current frame's Y-axis.
7. Angle $\phi$ - Angle to be rotated about the current frame's X-axis.

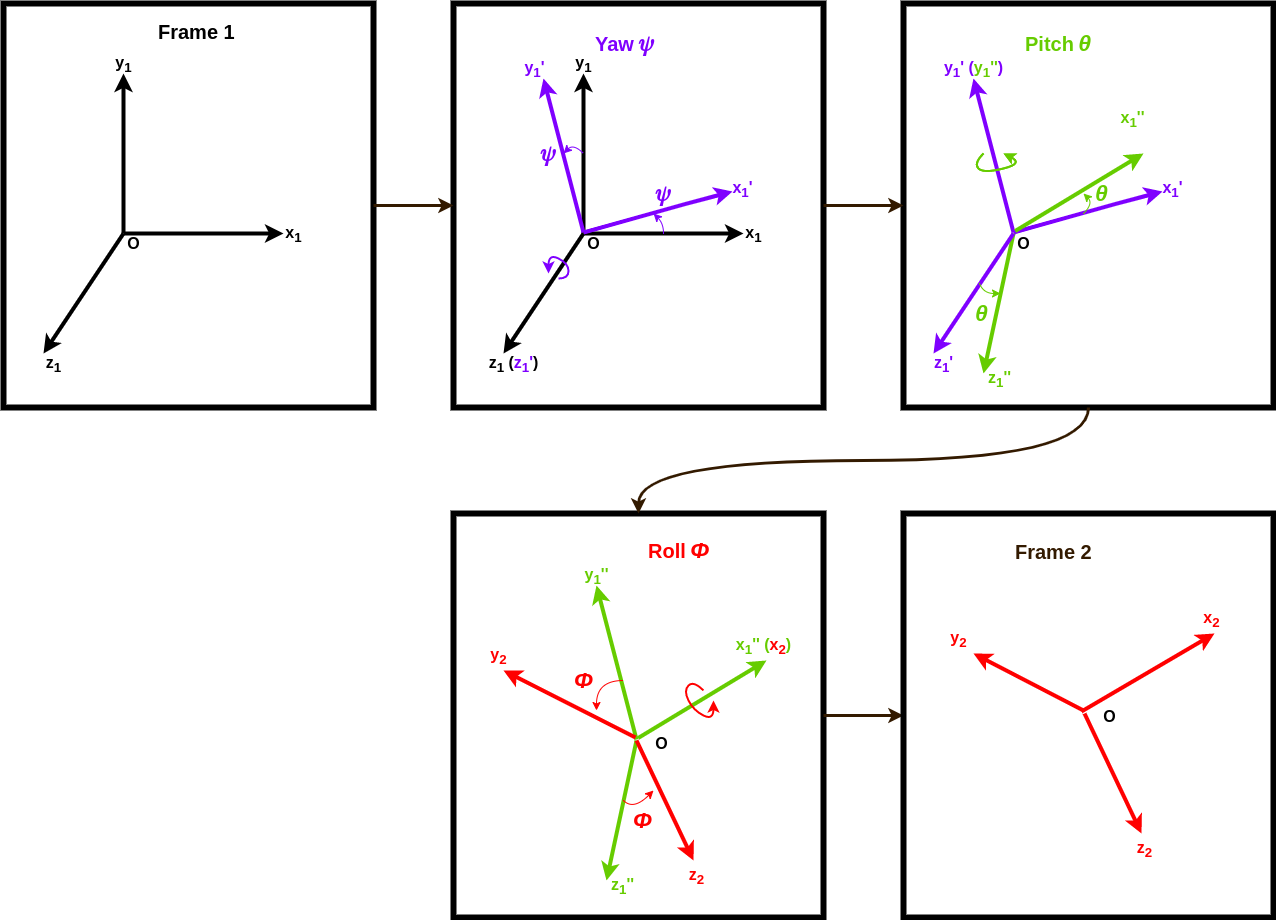
Sequence of rotation of three Euler angles:

Let’s say one has to go from frame 1 to frame 2 using Euler angle \(\psi\), \(\theta\), \(\phi\). Lets start with the current frame, i.e., frame 1.

1. Original Frame: $Ox_{1}y_{1}z_{1}$
2. Target Frame: $Ox_{2}y_{2}z_{2}$
3. Angle $\psi$ is the rotation about $Oz_{1}$.
   • This transformation takes frame $Ox_{1}y_{1}z_{1}$ to frame $Ox_{1}^{\prime}y_{1}^{\prime}z_{1}^{\prime}$
   • $Ox_{1}$ is rotated to $Ox_{1}^{\prime}$
   • $Oy_{1}$ is rotated to $Oy_{1}^{\prime}$
   • $Oz_{1}$ is rotated to $Oz_{1}^{\prime}$. The axes $Oz_{1}$ and $Oz_{1}^{\prime}$ overlap with each other.
   • One should note, $Oy_{1}^{\prime}$ now falls in the plane $Oy_{2}z_{2}$ and $Ox_{1}^{\prime}$ now falls in the plane $Ox_{2}z_{2}$. These two planes are in the target frame of reference.
4. Angle $\theta$ is rotation about $Oy_{1}^{\prime}$.
   • This transformation takes frame $Ox_{1}^{\prime}y_{1}^{\prime}z_{1}^{\prime}$ to frame $Ox_{1}^{\prime\prime}y_{1}^{\prime\prime}z_{1}^{\prime\prime}$.
   • $Ox_{1}^{\prime}$ is rotated to $Ox_{1}^{\prime\prime}$.
   • $Oy_{1}^{\prime}$ is rotated to $Oy_{1}^{\prime\prime}$. The axes $Oy_{1}^{\prime}$ and $Oy_{1}^{\prime\prime}$ overlap with each other.
   • $Oz_{1}^{\prime}$ is rotated to $Oz_{1}^{\prime\prime}$.
   • $Ox_{1}^{\prime\prime}$ now coincides with the axes $Ox_{2}$ and $Oz_{1}^{\prime\prime}$ now falls in the plane $Oy_{2}z_{2}$. The axis $Ox_{2}$ and the plane $Oy_{2}z_{2}$ are in the target frame of reference.
5. Angle $\phi$ is rotation about $Ox_{1}^{\prime\prime}$.
   • This transformation takes frame $Ox_{1}^{\prime\prime}y_{1}^{\prime\prime}z_{1}^{\prime\prime}$ to frame $Ox_{1}^{\prime\prime\prime}y_{1}^{\prime\prime\prime}z_{1}^{\prime\prime\prime}$. The resulting frame $Ox_{1}^{\prime\prime\prime}y_{1}^{\prime\prime\prime}z_{1}^{\prime\prime\prime}$ is also the target frame $Ox_{2}y_{2}z_{2}$.
   • $Ox_{1}^{\prime\prime}$ is rotated to $Ox_{1}^{\prime\prime\prime}$ ($Ox_{2}$).
   • $Oy_{1}^{\prime\prime}$ is rotated to $Oy_{1}^{\prime\prime\prime}$ ($Oy_{2}$).
   • $Oz_{1}^{\prime\prime}$ is rotated to $Oz_{1}^{\prime\prime\prime}$ ($Oz_{2}$).
   • $Oy_{1}^{\prime\prime\prime}$ now coincides with the axes $Oy_{2}$ and $Oz_{1}^{\prime\prime\prime}$ coincides with the axis $Oz_{2}$. The axes $Oy_{2}$ and $Oz_{2}$ are in the target frame of reference.

Constrains on three Euler angles:

Euler angle rotation using rotation matrices faces the issue of singularity or gimbal lock. These angle rotations are constraint to avoid ambiguities. The limits are as follows:

\[-\pi \le \psi \le \pi\] \[-\frac{\pi}{2} \le \theta \le \frac{\pi}{2}\] \[-\pi \le \phi \le \pi\]

Rotational Transformations

Let there be two frames defined as start frame and target frame.

• Start Frame: \(Ox_{1}y_{1}z_{1}\)
• Target Frame: \(Ox_{2}y_{2}z_{2}\)
• A point \(p\) is defined in the start and target frames as \(p^{1}\) and \(p^{2}\) respectively.

Now, with the help of Euler angles, transform the point given in the start frame to the corresponding point in the target frame.

Note: Order of transformation is: (1) Angle \(\psi\) along \(Oz_{1}\); (2) Angle \(\theta\) along \(Oy_{1}^{\prime}\); (3) Angle \(\phi\) along \(Ox_{1}^{\prime\prime}\).

• Rotation by \(\psi\) along \(Oz_{1}\): This transforms point \(p^{1}\) in frame \(Ox_{1}y_{1}z_{1}\) to point \(p^{1^{\prime}}\) in frame $Ox_{1}^{\prime}y_{1}^{\prime}z_{1}^{\prime}$.

\[p^{1^{\prime}} = R_{1_{z=\psi}}^{1\prime} p^{1}\]

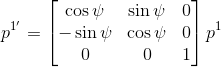
• The above transformation is followed by \(\theta\) around \(Oy_{1}^{\prime}\) and then by \(\phi\) around \(Ox_{1}^{\prime\prime}\).

\[p^{1^{\prime\prime}} = R_{1^{\prime}_{y=\theta}}^{1^{\prime\prime}} p^{1^{\prime}}\]

\[p^{2} = R_{1^{\prime\prime}_{x=\phi}}^{2} p^{1^{\prime\prime}}\]

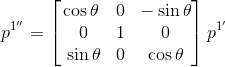
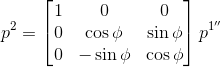
Therefore, the resultant transformation matrix for going from Frame \(Ox_{1}y_{1}z_{1}\) to Frame \(Ox_{2}y_{2}z_{2}\) is:

\[p^{2} = R_{1^{\prime\prime}_{x=\phi}}^{2} R_{1^{\prime}_{y=\theta}}^{1^{\prime\prime}} R_{1_{z=\psi}}^{1^{\prime}} p^{1}\]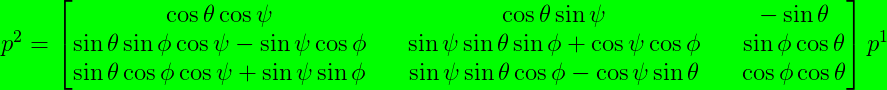

\[p^2 = R_1^2 p^1\]

Code

The code for euler angle transformation is available on Google Colab:

You can also find the corresponding notebook on github:

References

• Pamadi, B. N. (2004). Performance, stability, dynamics, and control of airplanes. American Institute of aeronautics and astronautics.