Quaternion Rotation

Quaternions are a number system that extends complex numbers. A quaternion provides a convenient mathematical notation for representing orientations and rotations of an object in three dimensions. This section discusses some of the useful properties and operations which are used in quaternion rotation.

Let there be two coordinate frames in a 3-dimensional space, \(A\) and \(B\). There is a vector \(r^{A}\) defined in Frame \(A\) as shown in figure below.

\[r^{A} = (r^{A}_{x}, r^{A}_{y}, r^{A}_{z})\]

Using Quaternions we can rotate from frame \(A\) to \(B\) by angle \(\theta\) around vector \(r^{A}\).

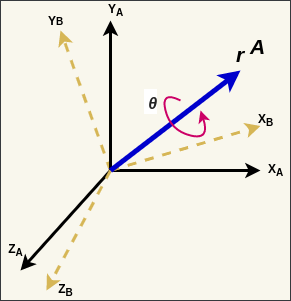
Quaternion describing this orientation is \(q^{A}_{B}\):

\[q^{A}_{B} = [q_1, q_2, q_3, q_4] = [cos(\frac{\theta}{2}), -r^{A}_{x} sin(\frac{\theta}{2}), -r^{A}_{y} sin(\frac{\theta}{2}), -r^{A}_{z} sin(\frac{\theta}{2})]\]

\(q^{A}_{B}\) describes the orientation of frame \(B\) relative to frame \(A\).

Quaternion arithmetic requires the quaternion describing orientation to be of unit length.
Therefore, quaternions are first normalized to have a magnitude of 1.

\[\parallel q \parallel_2 = 1\]

Conjugate quaternion:

\[^{*}q^{A}_{B} = q^{B}_{A} = [q_1, -q_2, -q_3, -q_4]\]

Compound orientations using quaternions: Let \(q^{A}_{B}\) and \(q^{B}_{C}\) be two quaternions. \(q^{A}_{B}\) - orientation of \(B\) w.r.t. \(A\).
\(q^{B}_{C}\) - orientation of \(C\) w.r.t. \(B\).

The compound orientation \(q^{A}_{C}\) is defined as:

\[q^{A}_{C} = q^{B}_{C} \bigotimes q^{A}_{B}\]

\(q^{A}_{C}\) - orientation of \(C\) w.r.t. \(A\).
\(\bigotimes\) represents quaternion product.

Quaternion Product:
Let \(p\) and \(q\) be two quaternions. Then the product of these two quaternions is:

\[p \bigotimes q = [p_1, p_2, p_3, p_4] \bigotimes [q_1, q_2, q_3, q_4]\] \[p \bigotimes q = \begin{pmatrix} p_1 q_1 - p_2 q_2 - p_3 q_3 - p_4 q_4 \\ p_1 q_2 + p_2 q_1 + p_3 q_4 - p_4 q_3 \\ p_1 q_3 - p_2 q_4 + p_3 q_1 + p_4 q_2 \\ p_1 q_4 + p_2 q_3 - p_3 q_2 + p_4 q_1 \end{pmatrix}^T\]

Quaternion product is not commutative, i.e., \(p \bigotimes q \ne q \bigotimes p\).

NOTE: I know there may be a lot of confusion in Quaternion mathematics. The blogpost by Fan Zheng provides an excellent overview of conventions used in Quaternion representations. [2]

References

1. Madgwick, S. (2010). An efficient orientation filter for inertial and inertial/magnetic sensor arrays. Report x-io and University of Bristol (UK), 25, 113-118. [link]
2. Zhang, F. (2017). Quaternion Conventions: Hamilton and JPL. [link]